
Betsy Ross and the American Flag
Folding/one-cutting a Betsy Ross star from a Square
Thanks to Arnold Tubis Department of Physics (Ret.), Purdue University, West Lafayette, IN Visiting Fellow, University of California San Diego, La Jolla, CA, and Crystal E. Mills, California Mathematics Council ComMuniCator, Clayton, CA for providing this information to ushistory.org.
Also see Two Conundrums Concerning the Betsy Ross Five-Pointed Star.
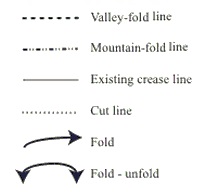
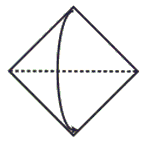
Step 1: Fold in half
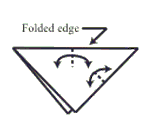
Step 2: Pinch crease in half the top and right side edges.
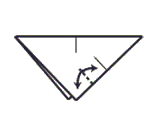
Step 3: Pinch crease in half the bottom half of the right side.
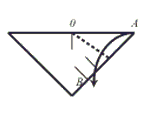
Step 4: Valley fold so that side OA
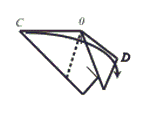
Step 5: Valley fold so that side OC is on top of sideOD
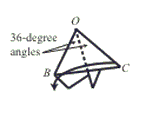
Step 6: Valley fold so that side OC is very nearly on top of side OB and the two folded edges on top just touch.
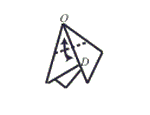
Step 7: Valley fold so that point O meets point D. Then unfold.
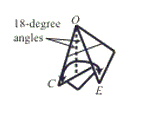
Step 8: Valley fold so that side OC meets side OE. Then unfold.
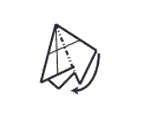
Step 9: Mountain fold the right section behind the left.
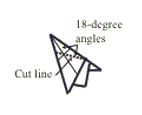
Step 10: Cut through all layers along the dotted line.

Step 11: The Betsy Ross Pentagram shape.
Notes
- The required folds (see steps 7 and 8) involve making creases for the perpendicular bisector of a line and an angle bisector. The geometric theorems involved are those relating to the properties of the perpendicular bisector of a line and isosceles triangles.
- The angle measures indicated in steps 6, 8, and 10 are rounded to the nearest integer. An analysis of the folding process for idealized paper shows that three of the five overlapping flaps in step 10 have apex angles of measure 35.782° and the apex angles of the other two are of measure 36.327°. For the case of real-world paper, these deviations from 36 degree measures are insignificant.


