
Betsy Ross and the American Flag
Folding/one-cutting a Betsy Ross star from 8-1/2 inch x 10 inch paper
Thanks to Arnold Tubis Department of Physics (Ret.), Purdue University, West Lafayette, IN Visiting Fellow, University of California San Diego, La Jolla, CA, and Crystal E. Mills, California Mathematics Council ComMuniCator, Clayton, CA for providing this information to ushistory.org.
Also see Two Conundrums Concerning the Betsy Ross Five-Pointed Star.
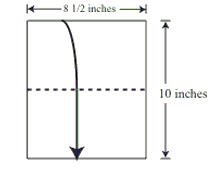
Step 1: Valley fold in half
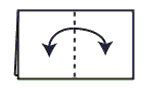
Step 2: Valley Fold in half. Unfold.
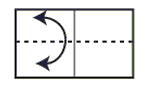
Step 3: Valley fold in half. Unfold.
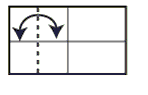
Step 4: Valley fold left section in half. Unfold.
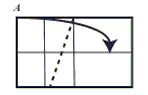
Step 5: Valley fold so that upper left point A touches the horizontal center line as shown in step 6.
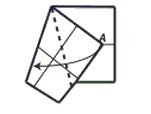
Step 6: Bring point A over to the left folded edge and valley fold.
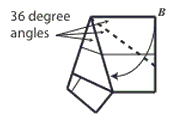
Step 7: Bring point B over to the indicated folded edge and valley fold.
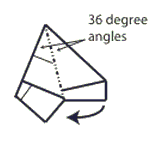
Step 8: Mountain fold the right section of the piece behind the left section.
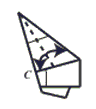
Step 9: Bisect the apex angle by valley folding so that point C is moved to the upper right edge of the piece. Then unfold.
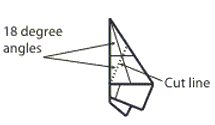
Step 10: Cut through all layers along the dotted line.

Step 11: The Betsy Ross Pentagram shape.


